La Riscoperta dei Solidi Platonici nel Rinascimento: Il “De divina proportione” di Luca Pacioli
Il “De divina proportione” di Luca Pacioli fu l’apice della riscoperta dei Solidi Platonici nel Rinascimento.
Prima di incontrare nuovamente un interesse così forte per i Solidi Platonici come quello manifestato tra il III e il II secolo a.C. in Grecia dobbiamo attendere l’Età del Rinascimento in Italia, tra XV e XVI secolo.
L’attenzione per la geometria solida continuò in epoca romana e, attraverso il contatto tra cultura bizantina e cultura islamica, nel Medioevo.
Tuttavia, le implicazioni filosofiche, estetiche e simboliche attinenti ai poliedri regolari vennero definitamene recuperate soltanto con l’Umanesimo.
Paolo Uccello tra Arte e Geometria

Un precursore del rinnovato connubio tra arte e geometria può considerarsi Paolo Uccello (1397-1475).
Fu artista singolare nelle cui opere convivevano il gusto tardogotico per la narrazione con l’allora recente metodo prospettico.

Pur non avendo lasciato trattati sistematici, si conosce il suo grande interesse per gli studi prospettici legati ai solidi geometrici e alla riduzione delle forme in strutture geometriche.
Anche se non ci sono rimaste testimonianze di sue elaborazioni dei Solidi Platonici, possediamo disegni di altri Solidi Geometrici complessi oltre che attribuzioni di opere di intarsio come:
il Mazzocchio, utilizzato in varie opere;
la Sfera a settantadue facce e punte, conservata a Parigi;
l’intarsio con il Piccolo Dodecaedro Stellato posto all’interno di un Cerchio di Esaedri, in S. Marco a Venezia.
I Trattati di Piero della Francesca
Tra i primi a interessarsi particolarmente dei Solidi Platonici vi fu Piero della Francesca (1416-1492).
Verso la fine della sua vita sostituì l’attività artistica con la trattatistica, scrivendo il “De abaco”, il “De quinque corporibus regularibus” e il “De prospectiva pingendi”.
Il “De abaco“, come venne chiamato in seguito, è principalmente un manuale di calcolo che coniuga la matematica applicata all’algebra e alla geometria.
Il “De quinque corporibus regularibus” riprende essenzialmente la geometria euclidea.
Esso tratta estesamente dei Cinque Solidi Platonici, interessandosi delle loro caratteristiche geometriche e tralasciando le implicazioni filosofiche e simboliche, pur partendo dall’opera di Platone.
Piero della Francesca si ispirò nel suo studio dell’argomento all’opera di Euclide, abbinandola a una visione più tecnica, consona all’operare artistico; utilizzò disegni geometrici dedicati ai cinque poliedri regolari e ad altri poliedri semiregolari.
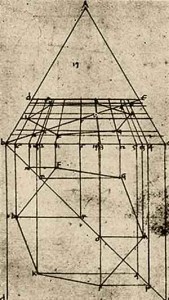
Il “De prospectiva pingendi” venne ispirato dal “De pictura” di Leon Battista Alberti, differenziandosi da questo per il tono più pratico che teorico.
Esso sviluppava ulteriormente gli argomenti del precedente trattato, presentandosi diviso in tre parti:
il “Disegno“, ovvero come disegnare le singole figure;
la “Commensurazio“, ovvero come disporre le figure nello spazio;
il “Coloro“, ovvero come colorare le figure in modo appropriato.
E’ soprattutto la seconda parte a presentare un’innovazione notevole rispetto ai trattati precedenti.
In essa ha particolare importanza l’assonometria; indagando la costruzione delle superfici e dei solidi geometrici, si arriva alla costruzione del corpo umano per mezzo della matematica.
L’opera teorica di Piero della Francesca fu basilare per il “De divina proportione” di Luca Pacioli e per il “Trattato della pittura” di Leonardo da Vinci.
Il “divulgatore” Luca Pacioli

Il frate francescano Luca Pacioli (1445-1517) può considerarsi il divulgatore in lingua volgare dei trattati matematici precedenti, soprattutto per mezzo del suo libro “Summa de Aritmetica, Geometria, Proportioni et Proportionalità“.
In esso spazia dalla matematica pura all’aritmetica mercantile e alla contabilità, illustrando per la prima volta il metodo della “partita doppia”.
L’opera che tuttavia esercitò maggiore influenza nel mondo dell’arte fu il “De divina proportione“, in cui viene rielaborato il trattato di Piero della Francesca (Vasari nelle sue “Vite”, accusa Pacioli addirittura di plagio).
Il manoscritto venne dedicato nel 1498 a Ludovico il Moro, signore di Milano, e quindi stampato a Venezia nel 1509.
“De divina proportione”:
Il Rapporto Aureo
Il titolo “De divina proportione” si riferisce a quella che si ottiene quando una linea viene divisa in un punto in due segmenti diseguali, in modo che il rapporto tra il minore e il maggiore sia pari al rapporto tra tale segmento maggiore e la linea intera iniziale.
Questo rapporto è lo stesso descritto da Euclide nel Libro VI degli “Elementi”, ed è lo stesso a cui si interessarono prima i Pitagorici e quindi Platone.
Dal XIX secolo questo rapporto viene chiamato Rapporto Aureo o Sezione Aurea ed è rappresentato dal numero irrazionale “phi“, ovvero 1,6180339887…
Grazie a questo rapporto è possibile realizzare il Pentagono, il Pentagramma e quindi due dei Solidi Platonici più complessi, l’Icosaedro e il Dodecaedro.
Quest’ultimo assunse particolare importanza nelle speculazioni neoplatoniche, a cui era partecipe anche Pacioli, che si rifacevano alla visione della materia e dell’universo espressa nel “Timeo” e nel “Fedone” platonici.
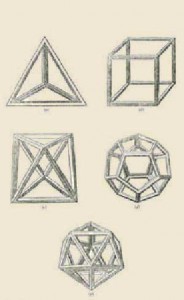
I Cinque Solidi Platonici e i Poliedri derivati
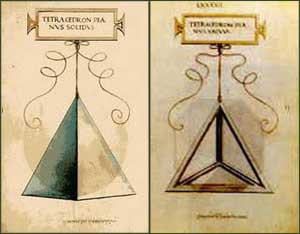
Nel “De divina proportione“, Pacioli presentò inoltre la dimostrazione matematica che non vi possono essere più di cinque poliedri regolari, corredandola di argomentazioni filosofiche.
Egli quindi descrisse la costruzione dei Cinque Solidi Platonici e degli altri Poliedri che da loro derivano.
Nell’opera questi ultimi vengono detti “forme derivate” e distinti in due tipi:
le “forme abscise“, ossia tagliate, che si ottengono tagliando gli spigoli dei poliedri regolari in modo da avere delle facce non più tutte uguali ma egualmente regolari; queste figure geometriche vengono chiamate anche “solidi semiregolari” o “solidi archimedei“;
le “forme elevate” o “forme puntude“, che si ottengono costruendo su ogni faccia di un poliedro regolare o semiregolare una piramide formata da triangoli equilateri.
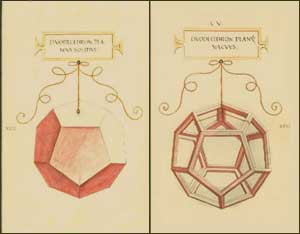
Di tutti questi solidi viene presentata la costruzione:
come “forma solida“, ossia piena;
come “forma vacua“, ossia vuota, ridotta agli spigoli.
Pacioli definì la sua opera, nella dedica a Ludovico il Moro, come: “…breve compendio e utilissimo tractato…sulle forme materiali de li corpi…a li viventi fin hora ascoste accompagnato da supreme e leggiadrissime figure de li platonici e mathematici corpi regulari che in prospectivo disegno non è possibile al mondo fare meglio…”
Leonardo da Vinci e il “De divina proportione”

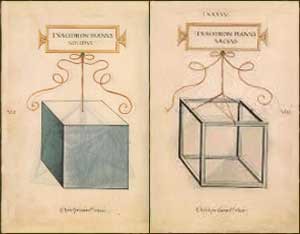
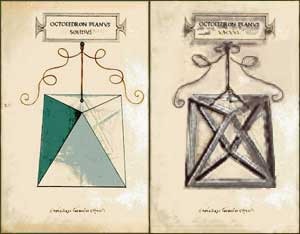
La parte conclusiva del “De divina proportione” è infatti composta da sessanta tavole illustrate derivanti direttamente da altrettanti disegni di Leonardo da Vinci.
Questi elaborò delle rappresentazioni tridimensionale e prospettiche dei poliedri, sia nella versione “solida” che in quella “vacua”, presentandoli sospesi a un sottile nastro e sormontati da un cartellino contenente il nome in lettere capitali romane.
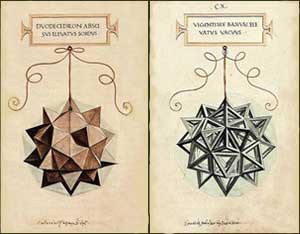
Gli originali di tali illustrazioni sono oggi perduti, benché Pacioli li avesse conservati con cura.
Di esse rimangono le copie del manoscritto e delle versioni a stampa.
La collaborazione tra Luca Pacioli e Leonardo da Vinci rappresenta la nuova visione della cultura che si stava formando in quell’epoca.
Il matematico aiutò l’artista fornendogli una esaustiva spiegazione degli “Elementi” di Euclide, che Leonardo fuse con gli insegnamenti prospettici pratici appresi dal Verrocchio e dai trattati dell’Alberti e di Piero della Francesca.
L’importanza scientifica della Prospettiva

Tale fruttuosa cooperazione fu possibile perché Pacioli stesso considerava il “disegno” fondamentale per recuperare queste entità matematiche e al contempo filosofiche e renderle comprensibili ai contemporanei.
Nel Capitolo III della stessa opera, l’autore infatti afferma: “…l’occhio esser la prima porta per la quale lo intelletto intende e gusta…”.

Tale frase esemplifica le seguenti necessità, comuni ad alcuni studiosi e artisti dell’epoca:
affermare il valore scientifico della Prospettiva, il nuovo modo di comprendere il mondo fisico;
accostarla alle classiche quattro Arti Liberali (Aritmetica, Geometria, Astronomia e Musica), svincolandola dal semplice ruolo tecnico.
Il “De divina proportione” e la cultura europea: Albrecht Dürer
Le illustrazioni del “De divina proportione” furono uno dei fattori decisivi per l’affermarsi dello studio scientifico della Prospettiva nel Nord d’Italia e in Europa.
Questo avvenne anche grazie al profondo interesse dimostrato per questi temi da Albrecht Dürer, che si trovò a Venezia nello stesso arco di anni in cui vi soggiornarono sia Leonardo da Vinci che Luca Pacioli (qualche studioso ha proposto di identificare il giovane alle spalle del frate nel famoso dipinto, attribuito a Jacopo de Barbari, con Dürer e non più con Guidobaldo da Montefeltro).
I Solidi Platonici e la Struttura dell’Universo nell’opera di Keplero
Dalla ripresa da parte degli Umanisti della filosofia neoplatonica nacque l’esigenza di dare forma matematica all’universo.
I concetti espressi da Luca Pacioli nel suo “De divina proportione” comunicano perfettamente questo bisogno di collegare le leggi che regolano l’universo a matematica, teologia e filosofia.

Questa mescolanza di intenti arrivò al massimo grado di speculazione nell’opera di Johannes Keplero (1571-1630), uno dei più grandi nomi dell’astronomia, a cui si devono tra l’altro le tre leggi del moto planetario che ne portano il nome.
Venuto a conoscenza, durante i suoi studi, del sistema eliocentrico di Copernico, egli lo trovò perfettamente corrispondente alla sua idea di universo e al suo tentativo di conciliare la teologia con la matematica e l’astronomia, nella convinzione che il Cosmo dovesse rispecchiare Dio.
Nello cosmologia copernicana, il Sole centrale era circondato dalla Sfera delle Stelle Fisse e separato da questa da uno Spazio Intermedio in cui orbitavano i Pianeti.
Per Keplero questa era una rappresentazione della Trinità: il Padre, il Figlio e lo Spirito Santo.
Fermamente convinto di dover contribuire alla comprensione del cosmo, inteso come creazione divina, egli cercò prima di tutto di rispondere alle seguenti domande:
Perché esistevano solo Sei Pianeti (nel sistema copernicano essi erano Saturno, Giove, Marte, Terra, Venere e Mercurio, mentre la Luna diventava il satellite della Terra)?
Perché le loro Orbite erano disposte proprio in quel modo?
La Visione del Cosmo in Keplero
Keplero elaborò la visione del Cosmo che doveva rispondere a queste domande partendo dall’osservazione delle Congiunzioni di Giove e Saturno, ovvero i momenti durante i quali i due pianeti hanno le stesse coordinate.
Egli notò che il rapporto tra il Raggio del Cerchio circoscritto in un Triangolo Equilatero e il Raggio del Cerchio inscritto nel medesimo Triangolo era quasi uguale al rapporto tra le dimensioni delle Orbite di Saturno e Giove.
Egli pensò pertanto di inscrivere ulteriormente un Quadrato per ottenere l’Orbita di Marte, ma i calcoli risultarono errati.
Trovò una soluzione soddisfacente utilizzando i Solidi Platonici.
Il “Mysterium Cosmographicum”
Kleplero espose le conclusioni a cui era giunto nel suo trattato “Mysterium Cosmographicum“.
I Pianeti erano Sei perché erano Cinque i Solidi Geometrici Regolari.
Se questi fossero considerati come dei limiti tridimensionali concentrici, darebbero origine a Sei Spazi.
La Successione di Pianeti e Solidi Platonici, dall’orbita più lontana dal Sole fino alla più vicina, era pertanto la seguente:
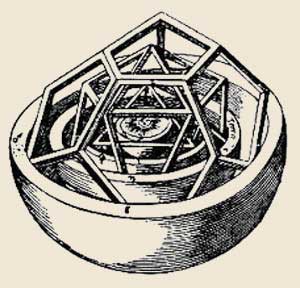
L’ORBITA DI SATURNO
L’ESAEDRO
L’ORBITA DI GIOVE
IL TETRAEDRO
L’ORBITA DI MARTE
IL DODECAEDRO
L’ORBITA DELLA TERRA
L’ICOSAEDRO
L’ORBITA DI VENERE
L’OTTAEDRO
L’ORBITA DI MERCURIO
Tramite questo modello dell’universo Keplero si sentiva in grado di risolvere anche il problema delle dimensioni delle orbite.
Egli infatti affermò nella stessa opera:
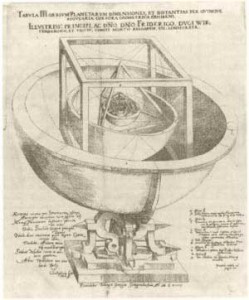
“… La sfera della Terra è la misura di tutte le altre orbite. Le si circoscriva un Dodecaedro. La sfera che lo circonda sarà quella di Marte. Si circoscriva un Tetraedro intorno a Marte. La sfera che lo circonda sarà quella di Saturno. Ora, si inscriva un Icosaedro nell’orbita della Terra. La sfera inscritta sarà quella di Venere. Si inscriva un Ottaedro dentro Venere. La sfera inscritta sarà quella di Mercurio…”
Nel “Mysterium Cosmographicum“, inoltre, la Terra separa:
i Solidi Platonici “stabili”, più lontani dal Sole, ovvero Dodecaedro, Tetraedro ed Esaedro;
dai Solidi Platonici “fluttuanti”, più vicini al Sole, ossia Icosaedro e Ottaedro.
Teologia e Astrologia in Keplero
I rapporti determinati da Keplero tra Pianeti e Solidi Platonici vennero da lui usati a conferma di postulati non solo scientifici ma anche teologici e astrologici.
In ambito teologico, egli pose la seguente analogia: come si presentano diversi gradi di differenza tra la Sfera e i vari Solidi Platonici, così si presentano le distinzioni tra il Creatore e gli Elementi del Creato.
Per quanto riguarda l’astrologia, Keplero non si discosta dalla cultura a lui contemporanea, che considerava questa disciplina una branca dell’astronomia: accettò la relazione tra corpi celesti e vita umana e pertanto ritenne il suo modello di cosmo valido anche per la speculazione astrologica.
Insuccesso della Teoria dei Solidi Platonici
La struttura del cosmo presentata nel “Mysterium Cosmographicum” non ebbe molto successo.
Sebbene, le distanze tra i pianeti ricavabili da questo modello risultassero corrispondenti ai dati allora disponibili, con un errore mediamente inferiore al 10%, tuttavia esso si dimostrò in altri punti inapplicabile.
Le successive osservazioni astronomiche compiute da Keplero stesso si dimostrarono in contrasto con la teoria dei Solidi Platonici e pertanto egli si vide costretto ad accantonarla.
Nonostante l’insuccesso finale, l’opera di Keplero rese attuale l’Idea Pitagorica de poter comprendere l’Universo per mezzo della Matematica e di poter spiegare con definiti Principi Fondamentali una molteplicità di Fenomeni; attraverso le proprietà dei Solidi Platonici si spiegavano il numero dei Pianeti, la loro disposizione e la misura delle loro orbite.
L’ “Harmonices mundi libri quinque”
Keplero si basò sulla medesima visione pitagorica per scrivere l’ “Harmonices mundi libri quinque“, dove convivevano Matematica, Musica e Astrologia.
Qui egli immaginò che le distanze armoniche tra i Pianeti fossero la prova della “musica delle sfere celesti” e che utilizzando il suo modello del cosmo si potessero comporre le Melodie dei Pianeti.
Nello stesso trattato Keplero:
enunciò la terza legge sul moto dei pianeti che porta il suo nome e che avrà notevole importanza per le successive ricerche di Newton;
si occupò di problemi di Geometria legati all’ “armonia“, interessandosi della “divina proportione” e del comportamento delle figure geometriche legate a questa, ad esempio nella tassellazione.
L’interesse dimostrato da Keplero per i Solidi Platonici può considerarsi l’ultimo atto del connubio tra metafisica, matematica e arte proposto nell’epoca del Rinascimento.
Nei secoli successivi queste discipline si allontaneranno gradualmente e la curiosità per queste figure geometriche riaffiorerà soprattutto nel XX secolo contemporaneamente al riavvicinarsi di matematica, scienza e arte.
